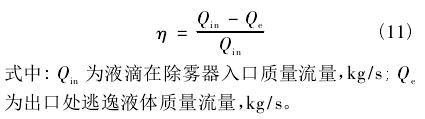采用欧拉-拉格朗日方法模拟了湿法烟气脱硫塔内折形板除雾器单通道二维流场的气液两相流动特性,气相采用SSTk-ω模型封闭的雷诺时均N-S方程,液滴采用颗粒随机轨道模型。在对无构件除雾器流场分析基础上,提出一种加装于除雾器叶片的构件,并分析了优化构件高度及顶角对气相流动特性、液滴运动轨迹及除雾器性能的影响。
模拟结果表明,所提出的新型构件可增强除雾器的捕集性能,构件高度由3mm增大至5mm或顶角由120°减小至60°均可进一步提高除雾效率,而高度的影响比顶角更加明显;综合考虑除雾效率与压降,对于高度为3mm或4mm的构件顶角适宜范围为90°至120°,而对于高度为5mm的构件,顶角减小使压降增加明显,其适宜角度为120°。
关键词:湿法烟气脱硫;除雾器;数值模拟;结构优化;除雾效率
湿法烟气脱硫(WetFlueGasDesulfurization,WFGD)技术已广泛应用于燃煤电厂SO2脱除,在我国已投运燃煤脱硫机组中石灰石-石膏法占90%以上[1]。
脱硫塔是WFGD系统的核心设备,烟气进入脱硫塔后与石灰石浆液逆流接触,SO2被雾化的液滴吸收,而烟气经浆液喷淋段后携带粒径小于500μm液滴,这部分浆液液滴不仅有可能引起下游设备的堵塞与酸腐蚀问题,而且存在使排烟含尘量超标的风险[2-3]。
除雾器安装于脱硫塔上部用于捕集烟气中夹带的液滴,但是对粒径较小液滴的分离效果较差[4],随着火电污染物排放限值的进一步降低,对除雾器的性能提出了更高的要求。因此,要实现除雾器的高效经济运行,对于除雾器的特性研究及结构优化至关重要[2-6]。
针对以上问题,王政允、黄新长、黄龙浩等[7-9]采用实验方法研究了不同板型、风速、叶片间距及液滴粒径分布条件下除雾装置的分离性能与压降特性,并分析了不同工况二次夹带的临界流速,但研究主要集中于除雾器的宏观特性分析,无法获得除雾器内部的流动细节。
相比实验研究方法,基于计算流体力学(Com-putationalFluidDynamics,CFD)的数值模拟方法可以预测除雾器通道内液滴的运动与烟气的流动特性,获取更全面的数据[10],因此众多研究者[2,11-13]将CFD技术引入除雾器内部流动分析,对除雾器影响因素、计算模型适用性等进行了大量研究。
Zamora等[11]分析了4种板型的波纹板除雾器性能,并对比了k-ε与k-ω模型的准确性,认为SSTk-ω模型计算结果更为准确;郝雅洁等[12]以文献[7-9]的实验数据作为参照,采用标准k-ε模型与颗粒随机轨道模型模拟了10μm至60μm液滴的运动特性及折形板除雾器叶片的捕集性能,结果表明除雾器对20μm以下液滴捕集效率较低;
洪文鹏等[2]基于RNGk-ε模型与颗粒随机轨道模型,研究了不同几何形状倒钩对折形板除雾器除雾效率与压损的影响;姚杰等[13]利用低Rek-ε模型计算分析了影响带倒钩波纹板性能的主要几何参数,认为叶片及倒钩几何特征对除雾效率及压降影响明显,并提出了高效的叶片结构几何参数的组合方式。
在以上研究基础上,本文针对折形板除雾器对小粒径液滴捕集性能较差的问题,提出一种流场优化构件,用于强化除雾器对10μm至30μm液滴的捕集,采用SSTk-ω模型对折形板除雾器原流场及优化后的流场进行计算,分析了通道内气液两相的流动特性,考察了构件几何因素对除雾效率与压降的影响。
1除雾器气液两相流动模型
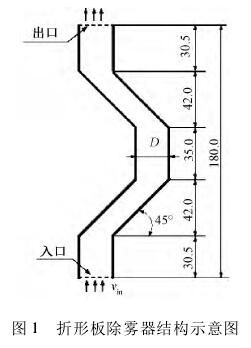
1.1模拟对象模拟对象为间距D=26mm折形板除雾器单通道流场,折形板除雾器叶片几何参数参考文献[12]数据,除雾器单通道及叶片结构如图1所示。
=
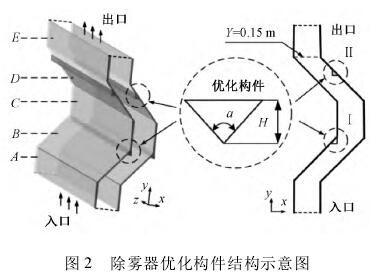
此外,本文在对原除雾器通道流场计算及分析的基础上,提出一种构件用以优化除雾器内气液两相流场(如图2),该构件分别加装于B段与D段。为考察构件结构对叶片除雾效率与压降特性的影响,模拟计算考虑的特征几何参数为有效高度H与顶角α,建立物理模型采用的H值为3mm、4mm、5mm,α值为60°、90°、120°。
1.2简化条件
除雾器叶片间形成的流动通道内为复杂的两相流,包含烟气流动、液滴自身破碎与液滴间碰撞、液滴与壁面碰撞引起的沉积与飞溅等复杂的物理过程,本文在误差允许范围内对两相流模型作如下简化:
(1)除雾器通道内烟气视为理想流动,且烟气马赫数小于0.1,故模拟的烟气为不可压缩流体[13];
(2)在脱硫塔等工业设备中除雾器叶片Z轴方向长度远大于其余两个维度,烟气流速在Z轴方向趋近于0,流场具有空间重复性[8,14],故将烟气流动视为二维平面流动;
(3)烟气经过喷淋层后为恒温饱和状态[15],因此忽略流动过程的热质传递;
(4)将烟气夹带的浆液液滴视为球形颗粒,并且忽略液滴的碰撞与破碎;
(5)根据文献[7-9]的实验数据,图1中所示的折形板除雾器发生液滴二次夹带的临界流速为6~7m/s,而本文采用的入口气速vin为3~6m/s,因此忽略烟气二次夹带的影响;
(6)液滴与除雾器叶片碰撞即视为被捕集,忽略因碰撞引起的液滴飞溅。
1.3气液两相流动的数学模型
本文采用欧拉-拉格朗日方法描述除雾器通道内气液两相的流体力学行为,其中烟气为连续流体,湍流模型选用SSTk-ω模型;液滴为离散项流体,模拟采用随机轨道模型。
对于连续相流动,视为粘性不可压缩定常流动。选取叶片间距D=26mm作为特征长度,各工况流动模型Re为5340至10680,低于Lauder与Spalding提出的临界雷诺数2×104,属于低雷诺数流动。连续相控制方程形式如下:
连续性方程
在湍流模型选取方面,Wang等[17]认为低雷诺数湍流模型相比STDk-ε模型可以更好地预测除雾器内的气液流动;Zamora等[11]、Galletti等[18]发现SST模型可更精确地模拟烟气的分离流动与二次流。
此外,上述文献研究结果均表明,准确模拟连续相流动对除雾器性能的预测具有重要意义。鉴于本文模拟的折形板加装构件后产生的分离流动现象更为明显,为了更准确地模拟烟气在除雾器内的低雷诺数流动以及因负压梯度引起的涡流,湍流模型选用SSTk-ω模型。
SSTk-ω湍流模型利用关于湍动能k与湍流频率ω的输运方程封闭雷诺时均处理的N-S方程组,对于定常流动其方程形式为:
对于液滴,模拟计算采用的液滴粒径为10~30μm,Saffman浮升力作用较明显[4],而液滴密度远高于烟气密度,可忽略附加质量力及Basset力等[17],本文仅考虑曳力、重力及浮力、Saffman浮升力与惯性力的平衡关系,液滴满足牛顿第二定律的控制方程为:
模拟液滴在流场中的运动采用随机轨道模型,考虑连续相湍流脉动引起的颗粒扩散效应,根据连续相的速度场分布,通过对方程(5)按一定时间步积分得到液滴在除雾器通道内的运动轨迹。
1.4计算参数及数值求解
数值计算采用AnsysFluent15.0作为计算平台,连续相的离散基于有限体积法,对流项离散格式为二阶迎风差分格式,计算采用SIMPLE算法,而对于离散项计算则采用拉格朗日方法。
1.5网格划分及无关性验证
由于液滴的捕集发生于壁面附近,而近壁面区域连续相流动对液滴运动具有明显的影响作用,因此选取恰当的近壁面处理方法及网格划分方式至关重要。Rafee等[20]认为增强壁面处理相比壁面函数法可以更精确地模拟低雷诺数流动;Zamora等[11]发现采用增强壁面处理方法时首层网格距壁面无量纲距离y+取值对除雾效率的计算结果影响明显,并建议首层节点y+适宜取值范围为0.2~0.5。
本文对连续相在近壁面区域计算采用增强壁面处理方法,利用ICEMCFD划分结构网格时,为提高流动计算的准确性,首层节点y+取值为0.5,该节点距壁面估计值为0.02mm。
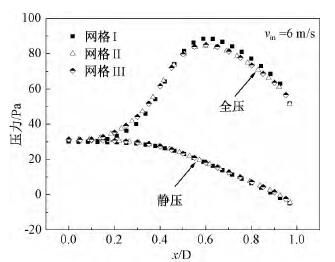
图3比较了入口气速vin为6m/s时2.8×104(网格I)、4.5×104(网格II)和6.8×104(网格III)三种结构网格在通道末端(Y=0.15m)沿X轴方向压力分布。可以发现2.8×104网格与其它网格的计算结果有较为明显的差别;网格数量由4.5×104增加约50%至6.8×104时计算结果吻合良好,因此最终确定网格数量为4.5×104。
图3Y=0.15m处静压与全压分布图
1.6两相间耦合方法对比
连续相与离散项的相互作用是两相流数值计算的重要因素之一。针对除雾器内液滴呈现稀疏离散相的特征[5],本文比较了入口气速vin为3m/s和6m/s时单向耦合与双向耦合方法对气相流动速度的影响。
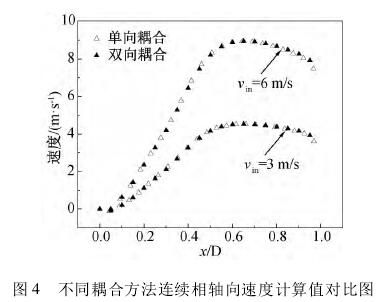
图4以dp=20μm粒径工况为例,给出连续相在Y=0.15m处轴向速度分量在X轴分布对比。
结果表明在不同入口气速条件下,两种耦合方法获得的流速分布差异很小,其他粒径在不同工况下也有类似特征。因此,脱硫塔除雾器通道内液滴的存在对烟气流动影响有限,连续相的运算迭代可忽略离散项。其他研究者在对脱硫塔除雾器[4]与冷却塔除雾器[17-18]内流场模拟时也忽略了液滴对气体流动的影响,采用单向耦合方法描述气液两相流动。
2结果与讨论
2.1无构件除雾器流场分析及优化
图5比较了入口气速为3m/s和6m/s时无构件折形板除雾器通道内气液两相的流动状态。模拟结果表明,连续相流经无构件除雾器通道时在C段及E段偏斜较为明显,其余段气相流动平缓,入口气速由3m/s增大至6m/s,尽管除雾器内气流平均流速有所提高,但连续相主流在通道内的流动状态较为相似,尤其C段与E段因气流偏斜形成的回流区范围未出现明显变化。
本文考察了无构件折形板除雾器对粒径dp为10μm、12.5μm、15μm、17.5μm、20μm、22.5μm、25μm、30μm共8种粒径液滴的捕集性能,以初始粒径dp=15μm液滴运动轨迹为例,选取500个液滴考察离散项的分布特性(见图5)。
当气速由3m/s增加至6m/s时,液滴在通道内的整体分布更为集中,分布范围略有减小,但是液滴运动轨迹并未发生明显变化,在不同入口气速条件下,液滴对气流均表现出较好的跟随性,其运动轨迹与主流近乎重合。
在液滴分布的局部特性方面,随气流运动的液滴与叶片B段与D段发生接触,且液滴集中分布在叶片附近;而在C段与E段仅有少数液滴因惯性离心力作用从气流中分离并与叶片碰撞,多数液滴则集中于除雾器通道中间处。
理论上,液滴惯性力随着气速升高呈现增大的趋势,这样可以增加液滴与叶片的碰撞几率从而提高除雾效率,但液滴分布显示仍有较多液滴从出口处逃逸,由式(11)计算得到入口为气速为3~6m/s时无构件除雾器对dp=15μm液滴的捕集效率均低于40%。
此外,二次夹带易发生于叶片折角处[21],对于本文模拟对象,多数液滴在D段被捕集并形成液膜,当有高速气流通过D、E段连接处折角时,气流对液膜的撕裂作用可能产生二次夹带,同时折角与出口间距离较短,没有足够长的叶片捕集气流夹带的液滴。
针对无构件除雾器对小粒径液滴分离效果较差的问题及可能出现的二次夹带问题,本文通过在叶片上加装构件(见图2)对折板除雾器通道内流场优化,旨在提高其除雾效率,同时其凸起结构使得流场内无流动死区,便于除雾器冲洗,降低结垢风险。
其中,构件I位于B段末端与C段的连接处,用于增强液滴的惯性力作用,从而提高C段捕集能力;构件Ⅱ位于D段,距离E段10~20mm,一方面其作用同构件I用于增大气流的偏转程度来提高液滴与E段的碰撞几率;另一方面,将构件Ⅱ与折角的位置设置一定间隔可避免折角处出现高速气流,降低二次夹带的可能性,也可在气流经D段偏转后使叶片有足够的长度用于捕集分离的液滴。
2.2构件高度对除雾器性能的影响
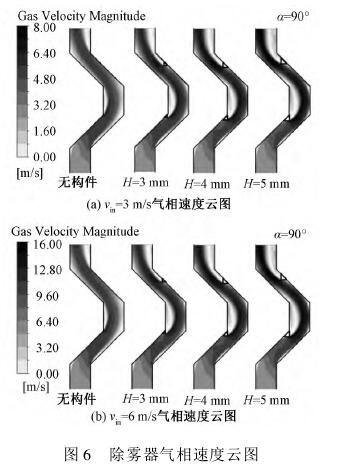
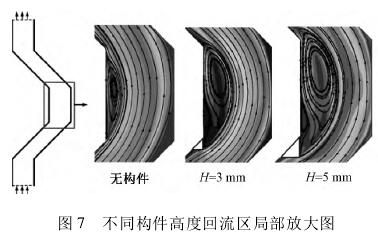
图6与图7分别为不同构件高度H时除雾器通道内气相速度云图与流动转折处局部放大图。
与无构件除雾器流场对比可知,优化构件可通过对气流施加扰动增强气流的偏转,同时气流偏折程度的变化使回流区的范围扩大,并且随着构件高度H增大,这一现象更为明显(图7);加装构件使转折后主流的流速升高,例如在气速vin=6m/s条件下,当H由3mm增至5mm时,通道内最高流速由13m/s提高至16m/s,这是由于回流区范围增大,主流因有效流通面积变小而流速升高。
此外,通过对比vin=3m/s与vin=6m/s时气相流动特性可知,在构件几何结构不变时,入口气速提高只对通道内气流的流速大小产生影响,而74气流的偏转及回流区范围未发生明显变化,这一特性与无构件除雾器相似。
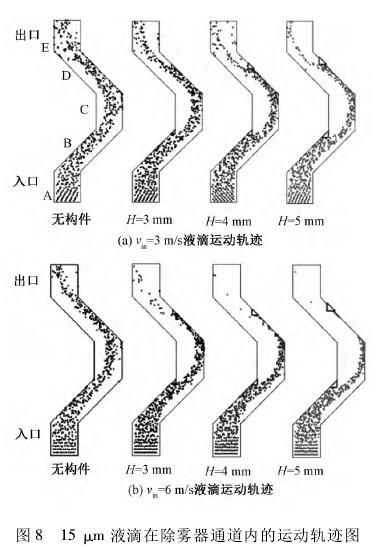
图8给出了构件高度H对粒径15μm液滴运动的影响,其中在每个通道内选取500个液滴作为分析对象。
当气速vin=3m/s时,液滴与除雾器叶片的接触主要出现在B段与D段,随H值增大,液滴运动轨迹的转折程度随之增大,D段的截留作用更加明显[13];当vin=6m/s时,无构件通道内液滴分布相对vin=3m/s变化较小,但随H的增大,液滴在经过B段后逐渐向右侧偏斜,并脱离气相主流,当H达到5mm时多数液滴在C段即被捕集,同时出口处液滴明显减少。
该现象表明,构件有效高度H增大,使气速对气液分离的影响更为明显。其原因主要为:一方面,构件的凸出结构可实现对气流夹带液滴的截留,液滴因惯性力被构件捕集,随气速增大,液滴的动量增大,截留作用更为明显,随H值增大,液滴与构件碰撞的几率增加;另一方面,随气速升高或H值增大,转折处回流区范围增大,气相主流流速升高伴随偏转加剧,随主流加速的液滴因惯性离心力增强与气相分离,从而提高了叶片的捕集性能。
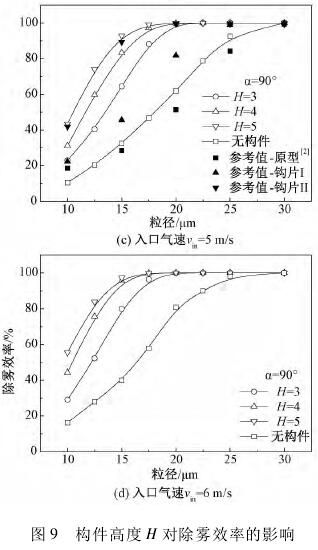
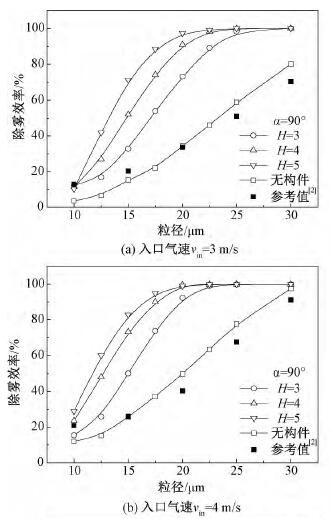
图9为不同气速条件下构件高度H对除雾效率的影响,无构件时本文对不同粒径液滴分离效率的模拟结果与洪文鹏等[2]的计算值偏差均小于10%。当内构件引入后,H值增大使除雾器对于各粒径液滴的脱除均有一定程度提高,在相同气速下构件对除雾效率的提升幅度随粒径增大而增加。
其原因主要是液滴所受阻力不足以平衡惯性离心力[22],由式(10)可以发现液滴弛豫时间τp随粒径增大而增加,构件对气流转折的强化使液滴对主流的跟随性变差[4],两相间出现滑移而导致气液分离,因此液滴更易被叶片捕集。
图9(c)给出了vin=5m/s工况下文献[2]中除雾器钩片与本文优化构件的除雾性能对比,其中钩片I长度4mm、宽度4mm;钩片II长度8mm、宽度4mm。结果表明钩片长度8mm时与H=4mm与5mm优化构件性能差别较小,而对15μm及20μm颗粒,钩片长度4mm时脱除性能相比于不同H值优化构件较差。
2.3构件顶角α对除雾器性能的影响
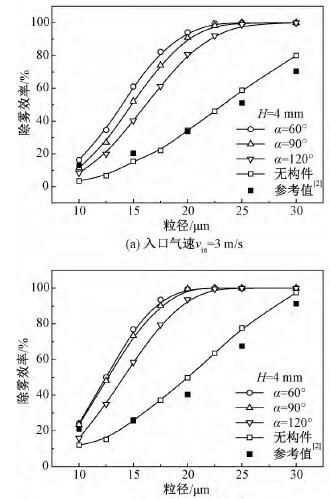
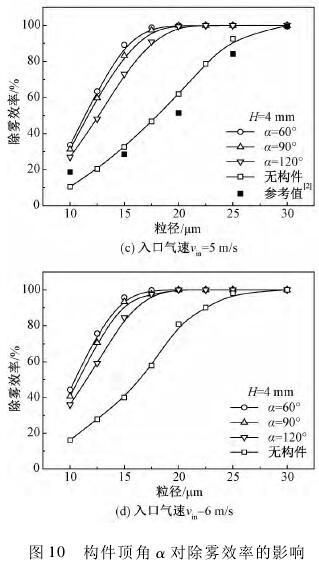
图10为不同气速下构件顶角α对除雾效率的影响。计算结果表明,当构件高度H一定时,各气速下顶角α值减小可提高除雾器对各粒径液滴的脱除效率。
以图11所示构件I附近流动为例分析其原因:当α=120°时气流经过构件后流动较为平缓,随着α减小,构件后连续相的负压梯度增大导致回流旋涡范围扩大,回流区的阻塞作用增强使得主流转折角增大且气相因通流截面减小而提速,从而使液滴因惯性离心作用增强而与气流分离。与构件高度H相比较,构件顶角α对除雾效率的影响较小。
例如,当入口气速vin=4m/s时H=3mm、α=120°对dp=17.5μm液滴脱除效率为65.26%;保持入口气速vin和构件高度H不变,当α减小到60°时脱除效率可以提高到81.21%,而保持入口气速vin和构件顶角α不变,H增大至5mm时除雾器对dp=17.5μm液滴脱除效率可高达92.04%。
2.4构件高度和顶角对压降的影响
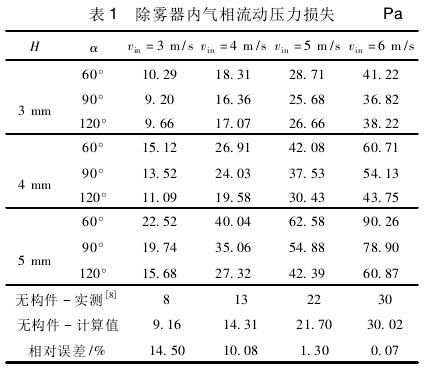
表1所示为不同工况下D=26mm折形板除雾器压力损失,对无构件除雾器压降计算结果与文献[7]实验数据吻合良好。定义附加压力损失为加装构件叶片压降与对应气速条件下无构件叶片压降的差值,当气速升高时,构件引起的附加损失增大,随H增大或α减小,这一损失进一步增大。
其原因为:气流经转折后形成二次流,在这一区域湍动能高,湍流耗散强烈[23],当构件几何结构不变,尽管气速升高时回流区范围变化并不明显(如图5、图6),但由于压力损失与流速的平方成正比,随气流速度的增大,因漩涡引起的压力损耗明显增加,因此压力损失因回流的能量损耗增大而升高[4];
当H增大时受构件扰动的气体流量增大,而当α减小时受扰动的气体沿X轴方向的速度分量增大,这两种效应均提高了转折气流的动量,使压力损失随回流区扩大而提高,同时,当α小于120°时,负压梯度增大,其挤压作用增强使旋涡进一步分离出壁角涡,随α减小壁角涡范围增大(如图11),这一现象也可能进一步引起能量损耗[23-24]。
当构件高度H=3mm,α由120°减小到90°时压降略有下降。其原因可能为:当构件高度较小时,α由120°减小到90°气流经过构件后形成旋涡形态略有改变,但回流范围较小,湍流耗散作用较弱,因此这部分能量耗散变化较小,而α=120°构件沿连续相流动方向长度较大,沿程阻力较高,致使其压力损失略高于α=90°构件。
此外,根据文献[2]计算值,vin=5m/s工况下加装除雾性能较好的钩片I时除雾器通道压降约为70Pa,高于表1所示各优化构件压降值,这是由于烟气不仅因转折产生额外压力损失,同时在钩片内侧形成回流,使气流的耗散增强[18]。
除雾效率与压降是除雾器性能的关键评价标准[2,4-6],综合考虑以上两种因素,对于H=3mm与H=4mm构件,α减小可提高除雾效率,同时α减小引起的压力损失较小,其适宜范围为90°≤α≤120°;对于H=5mm构件,α减小引起的压力损失有明显的增加,α=60°时构件引起压降相对于原通道压降可增加约200%,但相比压降变化,α减小对除雾效率改变较小(如图10),因此选用α=120°较为适宜。
3结论
本文利用数值模拟方法考察了构件结构H与α对气液两相流动的影响,所得结论如下:
(1)优化构件可通过截留作用捕集部分液滴,同时,构件引起的气流偏斜与主流区的加速可强化液滴从气流中分离,从而提高除雾效率。
(2)构件高度H提高或构件顶角α减小可强化气液相分离效率,提升叶片除雾性能,且H的影响比α更加明显。
(3)折形板除雾器加装构件后可提高气流的偏斜程度,扩大了回流区的范围,致使压力损失增大。综合考虑除雾效率与压降两种因素,构件几何因素的适宜取值为:对于H=3mm与H=4mm构件,α适宜范围为90°≤α≤120°;对于H=5mm构件,α适宜取值为α=120°。